Non tutti hanno avuto la possibilità di imparare a risolverle; per altri, invece, è trascorso tanto di quel tempo che non ci si ricorda bene i meccanismi che regolano queste operazioni.
Niente paura, proviamo insieme.
Per andare avanti con questo argomento dev'essere chiaro come si faccia la somma (o addizione) tra più numeri.
Sappiamo dire quanto fa 3 + 5? Oppure 20 + 13?
Se la risposta è sì, possiamo continuare!
Come si fanno le moltiplicazioni
Ecco una spiegazione semplice.
Moltiplicare un numero per un altro è come fare la somma di un numero tante volte quante sono quelle stabilite dall'altro numero. Un discorso un po' contorto, che sarà più chiaro con un facile esempio:
Esercizio 1
Risolviamo questa moltiplicazione: 3 x 2
Come abbiamo scritto prima si deve sommare uno dei numeri (ad esempio il 3) per un certo numero di volte (cioè 2).
Quindi 3 + 3 = 6 (ho sommato il numero 3 per 2 volte)
Il risultato viene anche se invertiamo i numeri, cioè se sommiamo il 2 per 3 volte.
Infatti: 2 + 2 + 2 = 6
In pratica la moltiplicazione non è altro che la somma dello stesso numero per se stesso.
Tornando all'esempio (3 x 2) che si può scrivere anche al contrario (2 x 3), proviamo a pensare a qualcosa di pratico, della vita di tutti i giorni.
Abbiamo 3 amici e vogliamo dare ad ognuno di loro 2 caramelle, quante caramelle dovremmo portarci dietro?
Sommando, dobbiamo fare 2 + 2 + 2, cioè 6. Ma abbiamo visto che è come se facessimo 3 x 2 (oppure 2 x 3).
Esercizio 2
Se volessimo, ad esempio, sommare il numero 4 per 10 volte, invece di scrivere 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4, potremmo abbreviare scrivendo semplicemente 4 x 10.
Un trucchetto, quindi. Ma valido solo quando si somma sempre il medesimo numero.
I numeri vengono chiamati fattori e il risultato è detto prodotto.
La moltiplicazione in colonna la scriviamo in questo modo:
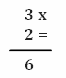
Per numeri così piccoli, fare la somma sembrerebbe ancora un metodo veloce. Ma cosa accade per numeri più grandi? Beh, qui, non ci sarebbe scampo, si deve per forza imparare a fare le moltiplicazioni!
Proviamo prima con un numero a due cifre e l'altro ancora ad una cifra.
Esercizio 3
Risolvere 11 x 3.
In questo caso, il sistema a colonna ci viene in aiuto, poiché permette di calcolare una parte per volta.

Infatti, senza calcolare direttamente il prodotto finale, possiamo moltiplicare il 3 prima per 1 (unità) e poi per l'altro 1 (decine), inserendo i risultati parziali uno di fianco all'altro, sotto la barra, come nell'esempio che segue:

Abbiamo fatto 3 x 1 = 3 e l'abbiamo inserito sotto la barra, a destra. Poi di nuovo il 3 x 1 = 3 e l'abbiamo inserito a sinistra. Questo schema è importante perché ci permette di calcolare un numero per volta, rispettando le colonne.
Il risultato finale è 33, quindi 11 x 3 dà come prodotto 33.
Esercizio 4
Proviamo con un esempio un po' più difficile, tipo questa moltiplicazione: 23 x 12

Il prodotto di 23 x 12 è uguale a 276. Ma com'è possibile?
Ricordiamo che si parte sempre dalle unità, poi si prosegue con le decine.
Prima di tutto abbiamo moltiplicato il "2" (del "12") prima per "3" (che fa "6") e poi per "2" (che fa "4"), esattamente come nell'esempio di prima, ottenendo "46", riportato sotto la prima barra.
Attenzione, però: abbiamo anche l'1 da moltiplicare. Come?
Seguiamo lo stesso procedimento, ma questa volta il risultato parziale lo mettiamo una riga sotto il "46" e spostato di una colonna a sinistra.
Quindi, 1 x 3 = 3 e poi 1 x 2 = 2, cioè "23".
Il 46 sopra e il 23 sotto, li abbiamo messi in modo tale da poter passare alla seconda fase, quella di somma.
Seguendo l'ordine per colonna (immaginiamo la prima colonna a destra formata solo dal "6", poi la colonna centrale dal "4" e dal "3", infine la colonna a sinistra dal "2"), calcoliamo le somme:
6 + 0 = 6 (unità)
4 + 3 = 7 (decine)
0 + 2 = 2 (centinaia)
Lo zero ("0") lo inseriamo per comodità, dove non ci sono numeri da sommare.
Il prodotto finale è "276".
Potrebbe capitare, però, che facendo le somme parziali (per colonna), si vada oltre il 10. In questo caso avremmo un numero a due cifre. Come si fa?
Esercizio 5
Iniziamo subito con un esempio difficilissimo: 123 x 456:

In pratica, ogni numero del secondo fattore (456) dobbiamo moltiplicarlo per ogni numero del primo fattore (123), spostando i risultati parziali di un posto verso sinistra.
Quindi, il primo risultato è calcolato moltiplicando il "6" per "3", poi per "2", poi per "1".
Il problema, che si presenta per la prima volta, è che (6 x 3) dà "18", un numero a due cifre. Ma noi possiamo mettere solo un numero ad una cifra. Come facciamo?
Semplice: scriviamo solo l'8 e riportiamo l'1 alla moltiplicazione successiva, che sarà (6 x 2).
(6 x 2 ) = 12 + 1 (che è l'uno di riporto, avanzato prima) = 13
Ecco, però, di nuovo un numero a due cifre. Ripetiamo allora lo stesso metodo: scriviamo il 3 e riportiamo l'1 all'altra moltiplicazione, cioè (6 x 1).
(6 x 1) = 6 + 1 (il riporto avanzato) = 7
Unendo i tre numeri abbiamo, nella prima riga sotto la barra, il risultato "738" (vedi schema in alto).
Stesso procedimento, per la riga successiva, ottenuta moltiplicando il "5" per "3", poi per "2", poi per "1".
(5 x 3) = 15, scrivo "5" e riporto di 1
(5 x 2) = 10 + 1 (riporto di prima) = 11, scrivo "1" e riporto di 1
(5 x 1) = 5 + 1 (riporto di prima) = 6
così ho il risultato della seconda riga: "615".
Nell'ultima riga, moltiplichiamo il "4" per "3", poi per "2", poi per "1".
(4 x 3) = 12, scrivo "2" e riporto di 1
(4 x 2) = 8 + 1 (riporto di prima) = 9 e scrivo "9" (qui non c'è la doppia cifra, quindi nessun riporto)
(4 x 1) = 4
quindi, nella terza riga avrò: "492"
Le tre righe ottenute (738 e 615 e 492), messe in colonna come nello schema in alto, sommando i numeri poi per colonna, danno come risultato finale: 56.088, cioè il prodotto di (123 x 456).
Per verificare i risultati potresti utilizzare la Prova del Nove.
Prova a leggere anche "Come moltiplicare un numero intero per 10, 100, 1000...", oppure Come calcolare la metà e il doppio di un numero, se sei interessato alle moltiplicazioni.


Nessun commento:
Posta un commento
Scrivi un commento qui sotto